Wide & Deep Learning 是由 Google Inc 发表的 paper <Wide & Deep Learning for Recommender Systems> 中提出的一种使用非线性特征的线性模型和一个用来 embedding 特征的深度学习进行联合训练 (joint training) 的方法[1]。
Introduction[2]
通过将稀疏数据的非线性转化特征引入到广义线性模型被广泛应用于大规模的回归和分类问题。使用交叉特征不仅强化了特征交互的记忆性,同时还提升了可解释性。然而,这增加了应用过程对特征进行操作的工作量。相对来说,通过从稀疏数据中学习低纬稠密的 embedding 特征,并应用到深度学习中,可以基于少量的特征工程实现对潜在的特征组合更好的泛化性。但是当用户项目交互是稀疏且高纬时,利用了 embeddings 的深度学习则表现得过于笼统 (over-generalize),推荐的都是些相关性很低的 items。在这篇文章中,提出了一个 wide & deep 联合学习模型,去结合推荐系统的 memorization和 generalization。
通过结合使用非线性特征的线性模型和用来 embedding 特征的深度学习,并且使用联合训练 (joint training) 的方法进行优化。主要思想基于交叉特征的线性模型只能从历史出现过的数据中找到非线性 (显性的非线性) ,深度学习可以找到没有出现过的非线性 (隐性的非线性) 。Memorization 通俗来讲就是把历史数据中显性的非线性找出来,而 generalization 就是通过找出隐性的非线性提高模型的泛化性。
推荐系统可以被看做是一个搜索排序系统,其中输入的 query 是一系列的用户和文本信息,输出是 items 的排序列表。给定一个 query,推荐的任务就是到数据库中去找出相关的 items,然后对这些 items 根据相关对象,如点击或者购买行为,并进行排序。
和传统的搜索排序问题一样,在推荐系统中一个挑战就是区域同时达到 memorization 和 generalization。Memorization 可以被大概定义为学习 items 或者 features 之间的相关频率,在历史数据中探索相关性的可行性。Generalizaion 的话则是基于相关性的传递,去探索一些在过去没有出现过的特征组合。基于 memorization 的推荐相对来说具有局部性,是在哪些用户和 items 已经有直接相关联的活动上。相较于 memorization,generalization 尝试去提高推荐 items 的多元化。
在工业中,对于大规模的在线推荐和排序系统,像逻辑回归这样的广义线性模型由于实现简单,可扩展性好,可解释性强而被广泛使用。通过喂给它一些 one-hot 编码的稀疏特征,比如二值特征 (user_installed_app=netfix) 表示用户安装了 Netflix。Memorization 则可以通过对稀疏特征做交叉积转换获得,就是求交叉特征。比如 AND 操作 (user_installed_app= netflix, impression_app=pandora) 这两个特征,当用户安装了Netflix并且之后展示在Pandora上,那么得到特征的值为1,其余为0。这个交叉特征展示了特征对之间的相关性和目标 lable 之间的关联。在逻辑回归上实现 generalization 可以通过增加一些粗粒度的特征实现,如 AND(user_installed_category=video, impression_category=music ),但是这些都是需要人工做特征工程实现,工作量极大。此外,cross-product transformation 的一个限制就是他们不能生成从未在训练数据中出现过的 query-item 特征对。
而 Embedding-based 的模型,比如因子分解机 (FM) 或深度神经网络,只需要很少的特征工程,通过为每个 query 和 item 特征对 (pair) 学到一个低维的 dense embedding vector,可以泛化到之前未见过的 query-item 特征对。但是如果潜在的 query-item 矩阵是稀疏,高秩的话,为 query 和 items 学习出一个有效的低纬表示往往很困难,比如基于特殊偏好的 users,或者一些很少出现的小众 items。在这种情况下,大多数的 query-item 没有交互,但是稠密的 embedding 还是会对全部的 query-item 对有非零的输出预测,因此能做出一些过泛化和做出一些不太相关的推荐。另一方面,利用交叉积特征 (cross-product features transformations) 的线性模型能用很少的参数记住那些异常规则 (exception_rules) 。
Wide & Deep Learning[3]
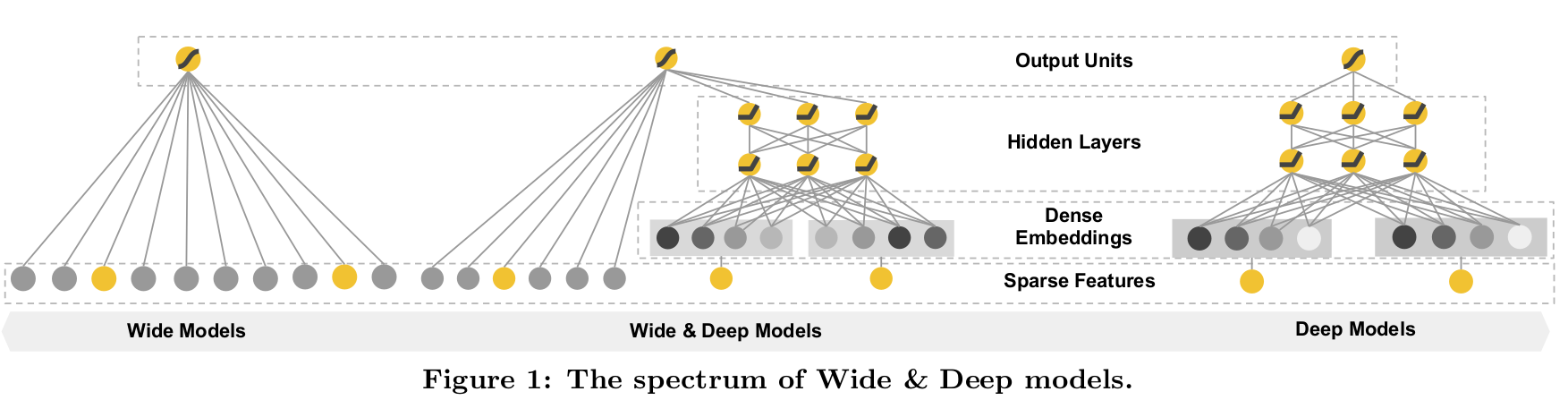
The Wide Component (Wide 组件)
Wide 组件是一个泛化的线性模型,$y=w^Tx+b$,如 Fig.1 图左所示。$y$ 是预测值,$x = [x_1, x_2, …, x_d]$ 是 $d$ 维特征向量,$w = [w_1, w_2,…, w_d]$ 是模型参数,$b$ 是 bias。特征集包括原始的输入特征和转换后 (cross-product transformation) 的特征。Cross-product transformation 有如下定义:
$$ \begin{aligned} \phi_k(x)=\prod_{i=1}^{d}x_{i}^{c_{ki}}, c_{ki} \in {0, 1} \end{aligned} \tag{1} $$
其中 $c_{ki}$ 为一个 boolean 变量,如果第 $i$ 个特征是第 $k$ 个变换 $\phi_k$ 的一部分,则为1,否则为0。对于二值特征,一个 cross-product transformation (比如:“AND(gender=female, language=en)”) 只能当组成特征 (“gender=female” 和 “language=en”) 都为1时才会为1, 否则为0。这可以捕获二值特征间的交叉,为通用的线性模型添加非线性 (显性的) 。
The Deep Component (Deep 组件)
Deep 组件是一个前馈神经网络 (feed-forward NN),如 Fig.1 图右所示。对于类别型特征,原始的输入是特征字符串 (比如:language=en) 。这些稀疏的、高维的类别型特征首先被转换成一个低维的、dense 的、real-valued 的向量,通常叫做 embedding vector。Embedding 的维度通常是 $O(10)$ 到 $O(100)$ 阶。该 embedding vectors 被随机初始化,接着通过最小化最终的 loss 的方式训练得到该值。这些低维的 dense embedding vectors 通过前向传递被 feed 给神经网络的隐层。特别地,每个隐层都会执行以下的计算:
$$ \begin{aligned} a^{l+1} = f(W^{(l)} a^{(l)} + b^{(l)}) \end{aligned} \tag2 $$
其中,$l$ 是层数,$f$ 是激活函数 (通常为ReLUs) ,$a(l)$,$b(l)$ 和 $W(l)$ 分别是第 $l$ 层的 activations,bias,以及 weights。
Wide & Deep 模型的联合训练
Wide 组件和 Deep 组件组合在一起,对它们的输入日志进行一个加权求和来做为预测,它会被 feed 给一个常见的 logistic loss function 来进行联合训练。注意,**联合训练 (joint training) 和集成训练 (ensemble) **有明显的区别。在 ensemble 中,每个独立的模型会单独训练,相互并不知道,只有在预测时会组合在一起。相反地,联合训练 (joint training) 会同时优化所有参数,通过将 wide 组件和 deep 组件在训练时进行加权求和的方式进行。这也暗示了模型的 size:对于一个 ensemble,由于训练是不联合的 (disjoint) ,每个单独的模型 size 通常需要更大些 (例如:更多的特征和转换) 来达到合理的精度。相比之下,对于联合训练 (joint training) 来说,wide 组件只需要补充 deep 组件的缺点,使用一小部分的 cross-product 特征转换即可,而非使用一个 full-size 的 wide 模型。
一个 Wide&Deep 模型的联合训练,通过对梯度进行后向传播算法、SGD 优化来完成。训练中使用 FTRL 算法和L1正则做为 Wide 组件的优化器,对 Deep 组件使用 AdaGrad。
组合模型如 Fig.1 图中所示。对于一个 logistic regression 问题,模型的预测为:
$$ P(Y = 1 | x) = \sigma(w_{wide}^{T} [x, \phi(x)] + w_{deep}^{T} a^{(l_f)} + b)\tag3 $$
其中 $Y$ 是二分类的 label,$\sigma(·)$ 是 sigmoid function, $\phi(x)$ 是对原始特征 $x$ 做 cross product transformations,$b$ 是 bias 项。$w_{wide}$ 是所有 wide 模型权重向量,$w_{deep}$ 是应用在最终激活函数 $a^{(l_f)}$ 上的权重。