什么是GBDT?
GBDT (Gradient Boosting Decision Tree) 是一种基于boosting集成学习(ensemble method)的算法,但相对于传统的Adaboost又有很大不同。在Adaboost,我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重。尽管GBDT也是迭代并且使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型,同时迭代思路和Adaboost也有所不同。GBDT选用的弱分类器一般是低方差高偏差,因为Boosting主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。GBDT的训练过程如下[1]:
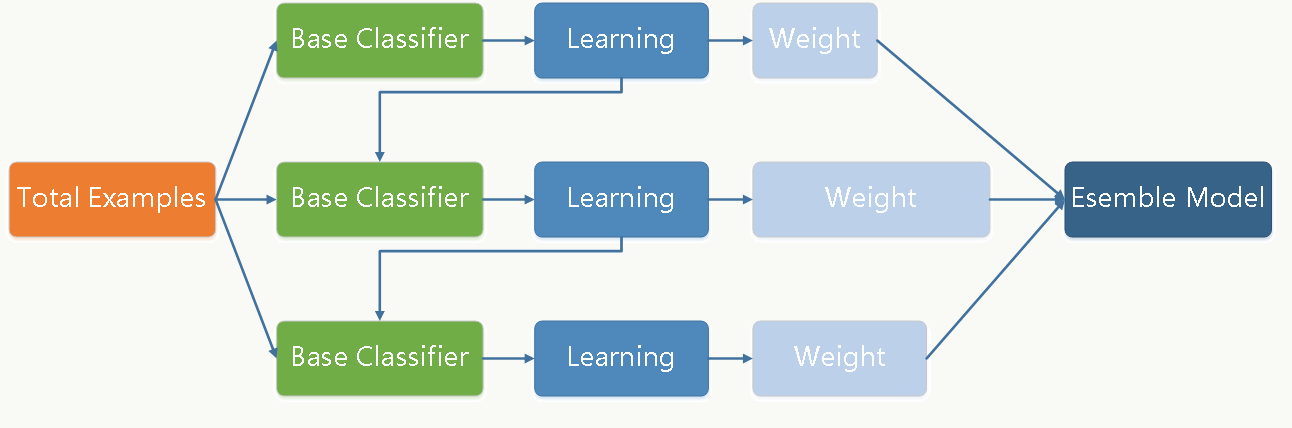
Boost
Boost是一个加法模型,它是由若干个基函数及其权值乘积之和的累加。
Gradient Boosting
GBDT把所有树的结论进行累加,从而获得最终结论,所以每棵树的结论并不是年龄本身,而是年龄的一个累加量。GBDT的核心就在于,每一棵树学习的是之前所有树结论和的残差,这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁,但第一棵树的预测年龄是12岁,差了6岁,即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习,如果第二棵树真的能把A分到6岁的叶子节点,那累加两棵树的结论就是A的真实年龄;如果第二棵树的结论是5岁,则A仍然存在1岁的残差,第三棵树里A的年龄就变成1岁,继续学。这就是Gradient Boosting在GBDT中的意义[2]。
根据上面那个简单的例子,我们知道假设损失函数为平方损失(square loss)时,我们使用残差来进行下一轮的训练,即GBDT算法的每一步在生成决策树时只需要拟合前面的模型的残差,从而使得损失函数最小。那如何使损失函数最小呢?Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值,进而拟合一个CART回归树,这就是GBDT的负梯度拟合。损失函数的负梯度在当前模型的值为:
$$ -[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}]{f(x)=f{m-1}(x)} \tag1 $$
Boosting的最大好处在于,每一步的残差计算其实变相地增大了分错样本的权重,而已经分对的样本则都趋向于0。因为对于已经分对的样本,其残差为0,在下一轮中几乎不起作用。
GBDT算法
知道了怎么解决损失函数拟合的问题,即GBDT的负梯度拟合之后,需要使用这些负梯度进行训练。假设$r_{mi}$表示第$m$轮的第$i$个样本的损失函数的负梯度:
$$ r_{mi} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{m-1} (x)}\tag2 $$
利用$(x_i,r_{mi})\quad(i=1,2,..n)$,我们可以拟合第$m$棵CART回归树,其对应的叶节点区域$R_{mj}, j =1,2,..., J$,其中$J$为叶子节点的个数。
针对每个叶子节点里的样本,我们求出损失函数最小,也就是拟合叶子节点最好的的输出值$c_{mj}$如下:
$$ c_{mj} = \underbrace{arg; min}_{c}\sum\limits_{x_i \in R_{mj}} L(y_i,f_{m-1}(x_i) +c)\tag3 $$
从而可以获得本轮的CART回归树的拟合函数:
$$ h_m(x) = \sum\limits_{j=1}^{J}c_{mj}I(x \in R_{mj})\tag4 $$
最后获得强学习器的表达式:
$$ f_{m}(x) = f_{m-1}(x) + \sum\limits_{j=1}^{J}c_{mj}I(x \in R_{mj})\tag5 $$
请结合上面的例子,理解每一轮更新强学习器都需要加上前面所有轮的输出!
GBDT回归算法
Freidman提出的梯度提升(Gradient Boosting)算法:利用最速下降的近似方法,即利用损失函数的负梯度在当前模型的值,作为回归问题中提升树算法的残差的近似值,拟合一个回归树。算法如下[3]:

算法步骤解释:
1、初始化,估计使损失函数极小化的常数值,它是只有一个根节点的树,即$\gamma$是一个常数值;
2、对于每轮CART回归树:
(a)计算损失函数的负梯度在当前模型的值,将它作为残差的估计
(b)估计回归树叶节点区域,以拟合残差的近似值
(c)利用线性搜索估计叶节点区域的值,使损失函数极小化
(d)更新回归树
3、得到输出的最终模型 $f(x)$。
GBDT分类算法
这里我们再看看GBDT分类算法,GBDT的分类算法从思想上和GBDT的回归算法没有区别,但是由于样本输出不是连续的值,而是离散的类别,导致我们无法直接从输出类别去拟合类别输出的误差[4]。
为了解决这个问题,主要有两个方法,一个是用指数损失函数,此时GBDT退化为AdaBoost算法。另一种方法是用类似于逻辑回归的对数似然损失函数。也就是说,我们用的是类别的预测概率值和真实概率值的差来拟合损失。本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数,我们又有二元分类和多元分类的区别。
二元GBDT分类算法
对于二元GBDT,如果用类似于逻辑回归的对数似然损失函数,则损失函数为:
$$ (y, f(x)) = log(1+ exp(-yf(x)))\tag6 $$
其中$y \in{-1, +1}$。此时的负梯度误差为:
$$ r_{mi} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{m-1};; (x)} = y_i/(1+exp(y_if(x_i)))\tag7 $$
对于生成的CART回归树,我们各个叶子节点的最佳残差拟合值为:
$$ c_{mj} = \underbrace{arg; min}_{c}\sum\limits_{x_i \in R_{mj}} log(1+exp(-y_i(f_{m-1}(x_i) +c)))\tag8 $$
由于上面的式子比较难优化,一般使用近似值代替:
$$ c_{mj} = \sum\limits_{x_i \in R_{mj}}r_{mi}\bigg / \sum\limits_{x_i \in R_{mj}}|r_{mi}|(1-|r_{mi}|)\tag9 $$
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,二元GBDT分类和GBDT回归算法过程相同。
多元GBDT分类算法
多元GBDT要比二元GBDT复杂一些,对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K,则此时我们的对数似然损失函数为:
$$ L(y, f(x)) = - \sum\limits_{k=1}^{K}y_klog;p_k(x)\tag{10} $$
其中如果样本输出类别为$k$,则$y_{k}=1$。第$k$类的概率$p_{k}(x)$的表达式为:
$$ p_k(x) = exp(f_k(x)) \bigg / \sum\limits_{l=1}^{K} exp(f_l(x))\tag{11} $$
集合上两式,我们可以计算出第$t$轮的第$i$个样本对应类别$l$的负梯度误差为:
$$ r_{mil} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f_k(x) = f_{l, m-1} (x)} = y_{il} - p_{l, m-1}(x_i)\tag{12} $$
观察上式可以看出,其实这里的误差就是样本$i$对应类别$l$的真实概率和$m−1$轮预测概率的差值。
对于生成的决策树,我们各个叶子节点的最佳残差拟合值为:
$$ c_{mjl} = \underbrace{arg; min}_{c_{jl}}\sum\limits_{i=0}^{m}\sum\limits_{k=1}^{K} L(y_k, f_{m-1, l}(x) + \sum\limits_{j=0}^{J}c_{jl} I(x_i \in R_{mj}))\tag{13} $$
由于上式比较难优化,我们一般使用近似值代替:
$$ c_{mjl} = \frac{K-1}{K} \frac{\sum\limits_{x_i \in R_{mjl}}r_{mil}}{\sum\limits_{x_i \in R_{mil}}|r_{mil}|(1-|r_{mil}|)}\tag{14} $$
除了负梯度计算和叶子节点的最佳残差拟合的线性搜索,多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同。